Στο χορό των Μοντέλων

Της Γεωργίας Πιστόλλα*

Τώρα και ένα χρόνο όλοι οι πολίτες συνεχώς ακούμε από τα ΜΜΕ για τα μοντέλα επιδημιών και τις προτάσεις της επιτροπής ειδικών στην πολιτική ηγεσία ώστε να εφαρμόζονται τα απαραίτητα μέτρα στην κοινωνία για την προφύλαξη της από τον ιό covid-19 , την λειτουργία της κοινωνίας αλλά και την αντιμετώπιση της πανδημίας.

Θεώρησα λοιπόν σκόπιμο να γράψω λίγα λόγια για τα μοντέλα , τη λειτουργία τους, πως και πότε  μαθαίνουμε από αυτά.

Θα σταθώ στα μοντέλα επιδημιών  ξεκινώντας από μια σύντομη ιστορική αναδρομή. 

Ιστορικά υπάρχουν αρκετές επιδημίες στο πέρασμα των χρόνων. Ξεκινώντας από τον Θουκυδίδη περιγράφεται η επιδημία της πανούκλας στην αρχαία Ελλάδα όπου 1.050 από τους 4.000 στρατιώτες πεθαίνουν. Ακόμη πιο τραγική είναι τον 19^ο αιώνα η επιδημία πανούκλας στην Ευρώπη όπου το 1/3 του τότε πληθυσμού πεθαίνει. Συνεχίζοντας στη σύγχρονη εποχή έχουμε την πανδημία HIV που οδηγεί στη νόσο AIDS.

Η μαθηματική λοιπόν μελέτη τέτοιων επιδημιών είναι σημαντική για διάφορους λόγους.

Θα πρέπει να τονίσω ότι ένα καλό μαθηματικό μοντέλο εξέλιξης μιας ασθένειας είναι αυτό που εμπεριέχει τα σημαντικότερα χαρακτηριστικά της και απορρίπτοντας τα όσα δεν είναι σημαντικά για να μπορεί να χρησιμοποιηθεί με αποτελεσματικότητα.

Όταν γίνεται μελέτη μιας πανδημίας πρέπει αρχικά να ξεχωρίσουμε τα άτομα του γενικού πληθυσμού ανάλογα με το αν νοσούν ή όχι. Συνεπώς μια συγκεκριμένη νόσο οδηγεί τον πληθυσμό  είτε σε ανοσία μετά από τη θεραπεία είτε σε θάνατο. Μετά από αυτή τη παρατήρηση ο ανθρώπινος πληθυσμός μπορεί να χωριστεί σε τρεις κατηγορίες :

1. Σε άτομα του πληθυσμού που είναι υγιή αλλά μπορούν να μολυνθούν. Τα άτομα αυτά ανήκουν στην ευπαθή ομάδα (Susceptibles) και έτσι προκύπτει και το πρώτο γράμμα S του μοντέλου .
2. Σε άτομα του πληθυσμού τα οποία νοσούν δηλ. είναι ασθενείς (Infectives) και έτσι προκύπτει και το δεύτερο γράμμα I του μοντέλου.
3. Σε άτομα του πληθυσμού τα οποία είτε έχουν θεραπευτεί και έχουν αποκτήσει ανοσία είτε έχουν πεθάνει και έτσι προκύπτει και το τρίτο γράμμα  R του μοντέλα.

Διαγραμματικά για ένα άτομο του πληθυσμού η εξέλιξη της νόσου είναι της μορφής:

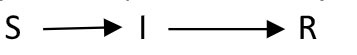
Κάθε μοντέλο έχει κάποιες προϋποθέσεις. Το συγκεκριμένο μοντέλο SIR το οποίο είχε προταθεί το 1927 από τους Kermack-McKendrick  βασίζεται στις τρεις παρακάτω παραδοχές : 1. Ο αριθμός των ασθενών-μολυσμένων αυξάνει ανάλογα με τον αριθμό των επαφών  μεταξύ ευπαθών και ασθενών με ένα γραμμικό όρο ως προς το γινόμενο rSI     2. Ο  αριθμός των ευπαθών αντίστοιχα μειώνεται ανάλογα με τον αριθμό των επαφών μεταξύ ασθενών και ευπαθών με τον όρο rSI και 

3. ο αριθμός των διαγραμμένων αυξάνει ανάλογα με τον αριθμό των ασθενών, κατά ένα ποσοστό aI, ενώ αντίστοιχα με το ίδιο ποσοστό μειώνεται ο αριθμός των ασθενών. 

Σύμφωνα λοιπόν με τις τρεις αυτές παραδοχές για το μοντέλο SIR  δημιουργήθηκε το μαθηματικό μοντέλο που αποτελείται από ένα σύστημα τριών συνήθων διαφορικών εξισώσεων, όπου r είναι ο ρυθμός διαγραφής και a  ο ρυθμός μόλυνσης και είναι θετικές σταθερές. Επίσης ορίστηκαν και οι αντίστοιχες αρχικές συνθήκες του μοντέλου. Δεν αναφέρω τις τρεις διαφορικές εξισώσεις αλλά απλώς τις περιέγραψα για να γίνει κατανοητό σε περισσότερους πολίτες.

Η κρίσιμη λοιπόν ερώτηση σε κάθε επιδημιολογική μελέτη την οποία καλείται και να απαντήσει είναι αν χρησιμοποιώντας το συγκεκριμένο μοντέλο , με τις συγκεκριμένες εξισώσεις, σταθερές και αρχικές συνθήκες που το περιγράφουν , επειδή αυτές περιγράφουν την ασθένεια και τον πληθυσμό, η ασθένεια θα εξαπλωθεί ή όχι , θα γίνει πανδημία ή όχι. Αποδεικνύεται μαθηματικά ότι η κρίσιμη παράμετρος που απαντά σε αυτό το ερώτημα δηλ. στην εξάπλωση ή μη της πανδημίας είναι ο λόγος p=a/r, καθώς και ο ρυθμός αναπαραγωγής της ασθένειας R_O = rSo/a. Ο ρυθμός αναπαραγωγής της ασθένειας αν θέλουμε να τον ερμηνεύσουμε σωστά εκφράζει, τον αριθμό των ατόμων σε ολόκληρο το πληθυσμό που μολύνονται από ένα μολυσμένο άτομο. Συνεπώς αν R_O >1 τότε από ένα μολυσμένο άτομο υπάρχουν περισσότερες από μία μολύνσεις και υπάρχει πανδημία.

Αυτό λοιπόν τον περίφημο δείκτη ακούμε όλο το διάστημα και είναι κυρίως αυτός σύμφωνα με τον οποίο ανακοινώνονται τα μέτρα. 

Συμπερασματικά : 

1. Υπάρχουν πολλά ακόμη μοντέλα όπως και μοντέλα που τροποποιούν αυτό στο οποίο αναφέρθηκα, ακόμη και SIR μοντέλα υποκατηγοριών.
2. Κάθε μοντέλο για να είναι όσο το δυνατόν έγκυρο θα πρέπει να έχει δεδομένα για τις μεταβλητές τις οποίες χρησιμοποιεί. Στο συγκεκριμένο μοντέλο για τον αριθμό των ευπαθών, μολυσμένων και διαγραμμένων και μάλιστα συνεχή και μεγάλο αριθμό δεδομένων. Σε διαφορετική περίπτωση γίνεται κατανοητό ότι δεν έχει αξία.
3. Μέχρι τώρα κανείς δεν έχει αναφερθεί στο όνομα του μοντέλου που χρησιμοποιεί, στις μεταβλητές του μοντέλου και στις αρχικές συνθήκες. Πολύ περισσότερο στο τρόπο συλλογής των δεδομένων και στην εγκυρότητα τους.
4. Οι χαμηλοί τόνοι σε αυτές τις περιπτώσεις είναι προτιμότεροι από τους υψηλούς.
5. Η απαραίτητη βιβλιογραφία σε ότι ακούγεται και από όπου ακούγεται είναι αναγκαία και αποτελεί απαραίτητο όρο για την επιστημονικότητα των λόγων κάθε ομιλούντα.
6. Για να λάβεις υπόψη σου τα αποτελέσματα του μοντέλου και να προχωρήσεις σε μέτρα (αν έχει χρησιμοποιηθεί σωστά το μοντέλο) πρέπει να δεις ποιες μεταβλητές σου πρέπει να βελτιώσεις και με ποιο τρόπο στη κοινότητα για να έχεις βελτίωση όλων των κοινωνικών πτυχών στην κοινότητα.
7. Άγνοια και μη διαφάνεια δε βοηθούν αλλά συμβάλλουν σε σενάρια που δεν βοηθούν τους δοκιμαζόμενους πολίτες αλλά και τη λύση του εκάστοτε προβλήματος.
8. Ας μας ανακοινώσουν λοιπόν όλοι αυτοί που χρησιμοποιούν μοντέλα, ποιο είναι το χρησιμοποιούμενο μοντέλο, ποια τα δεδομένα τους και ποια τα αποτελέσματα τους ως να έγραφαν άρθρο για δημοσίευση σε έγκριτο επιστημονικό περιοδικό. Τότε μόνο θα μπορούσε να αναπτυχθεί μια επιστημονική συζήτηση που θα στηρίζεται στην διαφάνεια και στην αγωνία όλων για καλύτερο αποτέλεσμα. Τέτοιου είδους επιστημονικές συζητήσεις με τη συμμετοχή επιστημών από πολλές ειδικότητες όπως, Μαθηματικούς, Βιολόγους, Ιατρούς, Οικονομολόγους, Ψυχολόγους, Επιδημιολόγους αλλά και εργαζόμενους σε δομές υγείας και δήμους θα συμβάλλει στην καλύτερη αντιμετώπιση της πανδημίας.

 Ενδεικτική Βιβλιογραφία: 

Ingalls, B. P. (2013) Mathematical Modeling is Systems Biology An introduction,MIT Press.

Κομηνέας, Σ., Χαρμανδάρης, Ε. (2015) Μαθηματική μοντελοποίηση.  Μια Σπουδή

στις Φυσικές Επιστήμες, Αθήνα, ΣΕΑΒ.

*Η Γεωργία Πιστόλλα είναι Μαθηματικός, Msc, Mba, Phd